Confusing Statistical Terms #11: Confounder

What is a Confounder?

Confounder (also called confounding variable) is one of those statistical terms that confuses a lot of people. Not because it represents a confusing concept, but because of how it’s used.

(Well, it’s a bit of a confusing concept, but that’s not the worst part).

It has slightly different meanings to different types of researchers. The definition is essentially the same, but the research context can have specific implications for how that definition plays out.

If the person you’re talking to has a different understanding of what it means, you’re going to have a confusing conversation.

Let’s take a look at some examples to unpack this.

Confounder as Perfectly Indistinguishable

In experimental fields, like agriculture and psychology, a confounder is a variable whose effect is indistinguishable from a independent variable’s effect.

An example:

You’re running a memory experiment and want to see whether people can better remember a list of easy to pronounce words or difficult to pronounce words. So you give one group of people a list of easy-to-pronounce words and another a list of difficult-to-pronounce words.

The variable you care about is the Word Pronounceability.

But it turns out that the difficult to pronounce words are also longer. If people remember fewer words from that list, you won’t know if ultimately it’s because they were harder to pronounce or simply because they were longer.

So Word Length is a confounding variable for Word Pronounceability for those lists of words.

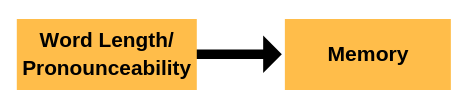
To truly be able to conclude that any memory difference is due to Pronounceability, you need to make sure the two lists of words are otherwise comparable in every other way. You either need both long and short words in both lists or you simply need both lists to only have, say, 5-letter words.

This is part of good experimental design.

Confounder as a Correlated Variable

Now, sometimes the issue is not bad design. Sometimes it’s truly impossible to separate out two variables that always co-occur.

For example, perhaps the confounding variable is not word length, but word frequency. People have an easier time pronouncing common words and a harder time pronouncing uncommon words.

So while your intention is to compare easy-to-pronounce words and hard-to-pronounce words, it’s possible there just aren’t any uncommon easy-to-pronounce words or any common hard-to-pronounce words to put on your list.

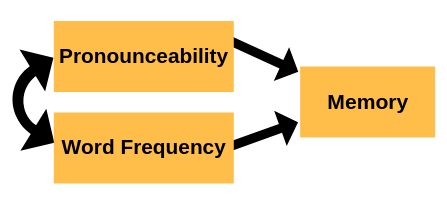
In other words, pronounceability and frequency of words are so associated, you can’t separate them out. We don’t know if words are more common because they’re easier to pronounce or if they’re easier to pronounce simply because they’re so common.

We just know we can’t separate them. So we don’t know which one is really at the heart of the relationship.

Confounder as a Causal Variable

The other definition I’ve seen of a confounding variable is more specific. I’ve heard this from people in fields like epidemiology where the variables are not manipulated, but measured.

In this situation, a confounding variable is one that is not only related to the independent variable, but is causing it.

So, for example, consider a study that is predicting infant birth weight from maternal weight gain during pregnancy.

And consider that there is a positive relationship. The more a mother gains during pregnancy, the more her baby weighs, on average.

But a potential confounder here is length of gestation. The longer the pregnancy lasts, the more time the mother and the baby have to gain weight.

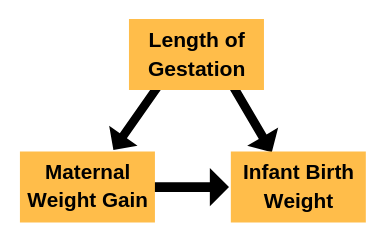
Now, in a data set that included only full-term infants, this may be only a minor issue. There may be little variance in maternal weight gain that came from length of the pregnancy.

But if the data set contains a lot of pre-term infants, then a lot of the variance in mother’s weight gain will come simply from how long her pregnancy was.

In this example, length of pregnancy is a confounder for weight gain. Another variable that’s related to weight gain, but not causing it, like mother’s age, is not considered a confounder.

Communicating about your variables

It’s a great practice to define your terms. It’s an essential practice when you’re communicating with people not in your field.

Since statistics is used across so many fields with so many data and design issues, it’s easy for the definitions of terms to become a bit insular. Everyone in your field may think of a confounder by one of these definitions, but your statistician or collaborators from other fields may have slightly different understandings. Make sure you’re using the same glossary.

Interpreting Linear Regression Coefficients: A Walk Through Output

Learn the approach for understanding coefficients in that regression as we walk through output of a model that includes numerical and categorical predictors and an interaction.

Take Me to The Video!