We’ve looked at the interaction effect between two categorical variables. Now let’s make things a little more interesting, shall we?
What if our predictors of interest, say, are a categorical and a continuous variable? How do we interpret the interaction between the two? (more…)
Transformations don’t always help, but when they do, they can improve your linear regression model in several ways simultaneously.
They can help you better meet the linear regression assumptions of normality and homoscedascity (i.e., equal variances). They also can help avoid some of the artifacts caused by boundary limits in your dependent variable — and sometimes even remove a difficult-to-interpret interaction.
(more…)
In a previous post we discussed using marginal means to explain an interaction to a non-statistical audience. The output from a linear regression model can be a bit confusing. This is the model that was shown.
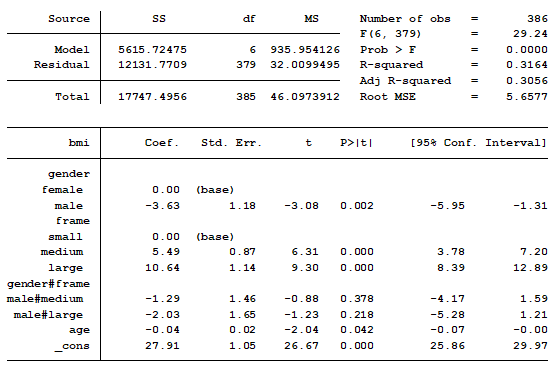
In this model, BMI is the outcome variable and there are three predictors:
(more…)
The concept of a statistical interaction is one of those things that seems very abstract. Obtuse definitions, like this one from Wikipedia, don’t help:
In statistics, an interaction may arise when considering the relationship among three or more variables, and describes a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of regression analyses.
First, we know this is true because we read it on the internet! Second, are you more confused now about interactions than you were before you read that definition? (more…)
If you have significant a significant interaction effect and non-significant main effects, would you interpret the interaction effect?
It’s a question I get pretty often, and it’s a more straightforward answer than most.
(more…)
One of those “rules” about statistics you often hear is that you can’t interpret a main effect in the presence of an interaction.
Stats professors seem particularly good at drilling this into students’ brains.
Unfortunately, it’s not true.
At least not always. (more…)


