 Level is a statistical term that is confusing because it has multiple meanings in different contexts (much like alpha and beta).
Level is a statistical term that is confusing because it has multiple meanings in different contexts (much like alpha and beta).
There are three different uses of the term Level in statistics that mean completely different things. What makes this especially confusing is that all three of them can be used in the exact same analysis context.
I’ll show you an example of that at the end.
So when you’re talking to someone who is learning statistics or who happens to be thinking of that term in a different context, this gets especially confusing.
Levels of Measurement
 The most widespread of these is levels of measurement. Stanley Stevens came up with this taxonomy of assigning numerals to variables in the 1940s. You probably learned about them in your Intro Stats course: the nominal, ordinal, interval, and ratio levels.
The most widespread of these is levels of measurement. Stanley Stevens came up with this taxonomy of assigning numerals to variables in the 1940s. You probably learned about them in your Intro Stats course: the nominal, ordinal, interval, and ratio levels.
Levels of measurement is really a measurement concept, not a statistical one. It refers to how much and the type of information a variable contains. Does it indicate an unordered category, a quantity with a zero point, etc?
So if you hear the following phrases, you’ll know that we’re using the term level to mean measurement level:
- nominal level
- ordinal level
- interval level
- ratio level
It is important in statistics because it has a big impact on which statistics are appropriate for any given variable. For example, you would not do the same test of association between two variables measured at a nominal level as you would between two variables measured at an interval level.
That said, levels of measurement aren’t the only information you need about a variable’s measurement. There is, of course, a lot more nuance.
Levels of a Factor
Another common usage of the term level is within experimental design and analysis. And this is for the levels of a factor. Although Factor itself has multiple meanings in statistics, here we are talking about a categorical independent variable.
In experimental design, the predictor variables (also often called Independent Variables) are generally categorical and nominal. They represent different experimental conditions, like treatment and control conditions.
Each of these categorical conditions is called a level.
Here are a few examples:
- In an agricultural study, a fertilizer treatment variable has three levels: Organic fertilizer (composted manure); High concentration of chemical fertilizer; low concentration of chemical fertilizer.So you’ll hear things like: “we compared the high concentration level to the control level.”
- In a medical study, a drug treatment has three levels: Placebo; standard drug for this disease; new drug for this disease.
- In a linguistics study, a word frequency variable has two levels: high frequency words; low frequency words.
Now, you may have noticed that some of these examples actually indicate a high or low level of something. I’m pretty sure that’s where this word usage came from. But you’ll see it used for all sorts of variables, even when they’re not high or low.
Although this use of level is very widespread, I try to avoid it personally. Instead I use the word “value” or “category” both of which are accurate, but without other meanings. That said, “level” is pretty entrenched in this context.
Level in Multilevel Models or Multilevel Data
A completely different use of the term is in the context of multilevel models. Multilevel models is a 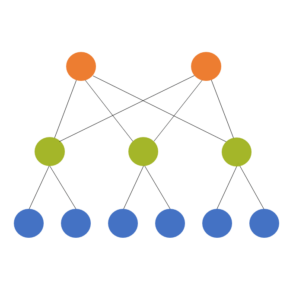 term for some mixed models. (The terms multilevel models and mixed models are often used interchangably, though mixed model is a bit more flexible).
term for some mixed models. (The terms multilevel models and mixed models are often used interchangably, though mixed model is a bit more flexible).
Multilevel models are used for multilevel (also called hierarchical or nested) data, which is where they get their name. The idea is that the units we’ve sampled from the population aren’t independent of each other. They’re clustered in such a way that their responses will be more similar to each other within a cluster.
The models themselves have two or more sources of random variation. A two level model has two sources of random variation and can have predictors at each level.
A common example is a model from a design where the response variable of interest is measured on students. It’s hard though, to sample students directly or to randomly assign them to treatments, since there is a natural clustering of students within schools.
So the resource-efficient way to do this research is to sample students within schools.
Predictors can be measured at the student level (eg. gender, SES, age) or the school level (enrollment, % who go on to college). The dependent variable has variation from student to student (level 1) and from school to school (level 2).
We always count these levels from the bottom up. So if we have students clustered within classroom and classroom clustered within school and school clustered within district, we have:
- Level 1: Students
- Level 2: Classroom
- Level 3: School
- Level 4: District
So this use of the term level describes the design of the study, not the measurement of the variables or the categories of the factors.
Putting them together
So this is the truly unfortunate part. There are situations where all three definitions of level are relevant within the same statistical analysis context.
I find this unfortunate because I think using the same word to mean completely different things just confuses people. But here it is:
Picture that study in which students are clustered within school (a two-level design). Each school is assigned to use one of three math curricula (the independent variable, which happens to be categorical).
So, the variable “math curriculum” is a factor with three levels (ie, three categories).
Because those three categories of “math curriculum” are unordered, “math curriculum” has a nominal level of measurement.
And since “math curriculum” is assigned to each school, it is considered a level 2 variable in the two-level model.
See the rest of the Confusing Statistical Terms series.
First published December 12, 2008
Last Updated January 21, 2025
 If you have a categorical predictor variable that you plan to use in a regression analysis in SPSS, there are a couple ways to do it.
If you have a categorical predictor variable that you plan to use in a regression analysis in SPSS, there are a couple ways to do it.
You can use the SPSS Regression procedure. Or you can use SPSS General Linear Model–>Univariate, which I discuss here. If you use Syntax, it’s the UNIANOVA command.
The big question in SPSS GLM is what goes where. As I’ve detailed in another post, any continuous independent variable goes into covariates. And don’t use random factors at all unless you really know what you’re doing.
So the question is what to do with your categorical variables. You have two choices, and each has advantages and disadvantages.
The easiest is to put categorical variables in Fixed Factors. SPSS GLM will dummy code those variables for you, which is quite convenient if your categorical variable has more than two categories.
However, there are some defaults you need to be aware of that may or may not make this a good choice.
The dummy coding reference group default
SPSS GLM always makes the reference group the one that comes last alphabetically.
So if the values you input are strings, it will be the one that comes last. If those values are numbers, it will be the highest one.
Not all procedures in SPSS use this default so double check the default if you’re using something else. Some procedures in SPSS let you change the default, but GLM doesn’t.
In some studies it really doesn’t matter which is the reference group.
But in others, interpreting regression coefficients will be a whole lot easier if you choose a group that makes a good comparison such as a control group or the most common group in the data.
If you want that to be the reference group in SPSS GLM, make it come last alphabetically. I’ve been known to do things like change my data so that the control group becomes something like ZControl. (But create a new variable–never overwrite original data).
It really can get confusing, though, if the variable was already dummy coded–if it already had values of 0 and 1. Because 1 comes last alphabetically, SPSS GLM will make that group the reference group and internally code it as 0.
This can really lead to confusion when interpreting coefficients. It’s not impossible if you’re paying attention, but you do have to pay attention. It’s generally better to recode the variable so that you don’t confuse yourself. And while you may believe you’re up for overcoming the confusion, why make things harder on yourself or with any other colleague you’re sharing results with?
Interactions among fixed factors default
There is another key default to keep in mind. GLM will automatically create interactions between any and all variables you specify as Fixed Factors.
If you put 5 variables in Fixed Factors, you’ll get a lot of interactions. SPSS will automatically create all 2-way, 3-way, 4-way, and even a 5-way interaction among those 5 variables.
That’s a lot of interactions.
In contrast, GLM doesn’t create by default any interactions between Covariates or between Covariates and Fixed Factors.
So you may find you have more interactions than you wanted among your categorical predictors. And fewer interactions than you wanted among numerical predictors.
There is no reason to use the default. You can override it quite easily.
Just click on the Model button. Then choose “Custom Model.” You can then choose which interactions you do, or don’t, want in the model.
If you’re using SPSS syntax, simply add the interactions you want to the /Design subcommand.
So think about which interactions you want in the model. And take a look at whether your variables are already dummy coded.
One of the difficult decisions in mixed modeling is deciding which factors are fixed and which are random. And as difficult as it is, it’s also very important. Correctly specifying the fixed and random factors of the model is vital to obtain accurate analyses.
Now, you may be thinking of the fixed and random effects in the model, rather than the factors themselves, as fixed or random. If so, remember that each term in the model (factor, covariate, interaction or other multiplicative term) has an effect. We’ll come back to how the model measures the effects for fixed and random factors.
Sadly, the definitions in many texts don’t help much with decisions to specify factors as fixed or random. Textbook examples are often artificial and hard to apply to the real, messy data you’re working with.
Here’s the real kicker. The same factor can often be fixed or random, depending on the researcher’s objective. (more…)
Multilevel models and Mixed Models are generally the same thing. In our recent webinar on the basics of mixed  models, Random Intercept and Random Slope Models, we had a number of questions about terminology that I’m going to answer here.
models, Random Intercept and Random Slope Models, we had a number of questions about terminology that I’m going to answer here.
If you want to see the full recording of the webinar, get it here. It’s free.
Q: Is this different from multi-level modeling?
A: No. I don’t really know the history of why we have the different names, but the difference in multilevel modeling (more…)
Part 1 outlined one issue in deciding whether to put a categorical predictor variable into Fixed Factors or Covariates in SPSS GLM. That issue dealt with how SPSS automatically creates dummy variables from any variable in Fixed Factors.
There is another key default to keep in mind. SPSS GLM will automatically create interactions between any and all variables you specify as Fixed Factors.
If you put 5 variables in Fixed Factors, you’ll get a lot of interactions. SPSS will automatically create all 2-way, 3-way, 4-way, and even a 5-way interaction among those 5 variables. (more…)
The beauty of the Univariate GLM procedure in SPSS is that it is so flexible. You can use it to analyze regressions, ANOVAs, ANCOVAs with all sorts of interactions, dummy coding, etc.
The down side of this flexibility is it is often confusing what to put where and what it all means.
So here’s a quick breakdown.
The dependent variable I hope is pretty straightforward. Put in your continuous dependent variable.
Fixed Factors are categorical independent variables. It does not matter if the variable is (more…)
 Level is a statistical term that is confusing because it has multiple meanings in different contexts (much like alpha and beta).
Level is a statistical term that is confusing because it has multiple meanings in different contexts (much like alpha and beta). The most widespread of these is levels of measurement. Stanley Stevens came up with this taxonomy of assigning numerals to variables in the 1940s. You probably learned about them in your Intro Stats course: the nominal, ordinal, interval, and ratio levels.
The most widespread of these is levels of measurement. Stanley Stevens came up with this taxonomy of assigning numerals to variables in the 1940s. You probably learned about them in your Intro Stats course: the nominal, ordinal, interval, and ratio levels. term for some mixed models. (The terms multilevel models and mixed models are often used interchangably, though mixed model is a bit more flexible).
term for some mixed models. (The terms multilevel models and mixed models are often used interchangably, though mixed model is a bit more flexible).


 models,
models,