In my last post I used the glm() command in R to fit a logistic model with binomial errors to investigate the relationships between the numeracy and anxiety scores and their eventual success.
Now we will create a plot for each predictor. This can be very helpful for helping us understand the effect of each predictor on the probability of a 1 response on our dependent variable.
We wish to plot each predictor separately, so first we fit a separate model for each predictor. This isn’t the only way to do it, but one that I find especially helpful for deciding which variables should be entered as predictors.
model_numeracy <- glm(success ~ numeracy, binomial)
summary(model_numeracy)
Call:
glm(formula = success ~ numeracy, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5814 -0.9060 0.3207 0.6652 1.8266
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.1414 1.8873 -3.254 0.001138 **
numeracy 0.6243 0.1855 3.366 0.000763 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 50.291 on 48 degrees of freedom
AIC: 54.291
Number of Fisher Scoring iterations: 5
We do the same for anxiety.
model_anxiety <- glm(success ~ anxiety, binomial)
summary(model_anxiety)
Call:
glm(formula = success ~ anxiety, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8680 -0.3582 0.1159 0.6309 1.5698
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.5819 5.6754 3.450 0.000560 ***
anxiety -1.3556 0.3973 -3.412 0.000646 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 36.374 on 48 degrees of freedom
AIC: 40.374
Number of Fisher Scoring iterations: 6
Now we create our plots. First we set up a sequence of length values which we will use to plot the fitted model. Let’s find the range of each variable.
range(numeracy)
[1] 6.6 15.7
range(anxiety)
[1] 10.1 17.7
Given the range of both numeracy and anxiety. A sequence from 0 to 15 is about right for plotting numeracy, while a range from 10 to 20 is good for plotting anxiety.
xnumeracy <-seq (0, 15, 0.01)
ynumeracy <- predict(model_numeracy, list(numeracy=xnumeracy),type="response")
Now we use the predict() function to set up the fitted values. The syntax type = “response” back-transforms from a linear logit model to the original scale of the observed data (i.e. binary).
plot(numeracy, success, pch = 16, xlab = "NUMERACY SCORE", ylab = "ADMISSION")
lines(xnumeracy, ynumeracy, col = "red", lwd = 2)
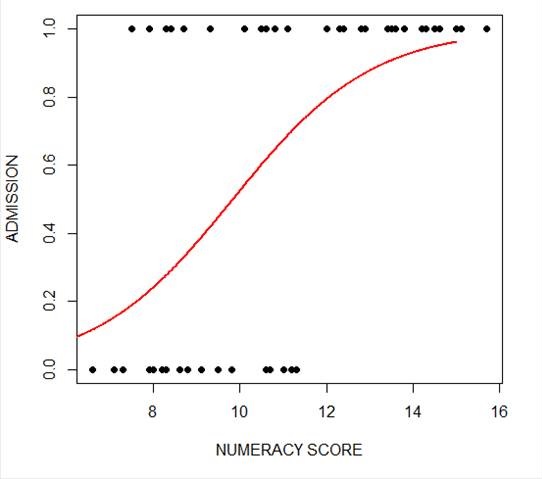 The model has produced a curve that indicates the probability that success = 1 to the numeracy score. Clearly, the higher the score, the more likely it is that the student will be accepted.
The model has produced a curve that indicates the probability that success = 1 to the numeracy score. Clearly, the higher the score, the more likely it is that the student will be accepted.
Now we plot for anxiety.
xanxiety <- seq(10, 20, 0.1)
yanxiety <- predict(model_anxiety, list(anxiety=xanxiety),type="response")
plot(anxiety, success, pch = 16, xlab = "ANXIETY SCORE", ylab = "SUCCESS")
lines(xanxiety, yanxiety, col= "blue", lwd = 2)
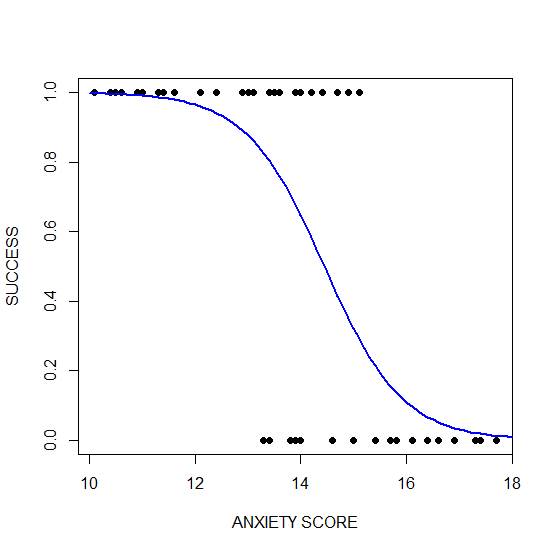 Clearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety.
Clearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety.
****
See our full R Tutorial Series and other blog posts regarding R programming.
About the Author: David Lillis has taught R to many researchers and statisticians. His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. David holds a doctorate in applied statistics.
Last year I wrote several articles (GLM in R 1, GLM in R 2, GLM in R 3) that provided an introduction to Generalized Linear Models (GLMs) in R.
As a reminder, Generalized Linear Models are an extension of linear regression models that allow the dependent variable to be non-normal.
In our example for this week we fit a GLM to a set of education-related data.
Let’s read in a data set from an experiment consisting of numeracy test scores (numeracy), scores on an anxiety test (anxiety), and a binary outcome variable (success) that records whether or not the students eventually succeeded in gaining admission to a prestigious university through an admissions test.
We will use the glm() command to run a logistic regression, regressing success on the numeracy and anxiety scores.
A <- structure(list(numeracy = c(6.6, 7.1, 7.3, 7.5, 7.9, 7.9, 8,
8.2, 8.3, 8.3, 8.4, 8.4, 8.6, 8.7, 8.8, 8.8, 9.1, 9.1, 9.1, 9.3,
9.5, 9.8, 10.1, 10.5, 10.6, 10.6, 10.6, 10.7, 10.8, 11, 11.1,
11.2, 11.3, 12, 12.3, 12.4, 12.8, 12.8, 12.9, 13.4, 13.5, 13.6,
13.8, 14.2, 14.3, 14.5, 14.6, 15, 15.1, 15.7), anxiety = c(13.8,
14.6, 17.4, 14.9, 13.4, 13.5, 13.8, 16.6, 13.5, 15.7, 13.6, 14,
16.1, 10.5, 16.9, 17.4, 13.9, 15.8, 16.4, 14.7, 15, 13.3, 10.9,
12.4, 12.9, 16.6, 16.9, 15.4, 13.1, 17.3, 13.1, 14, 17.7, 10.6,
14.7, 10.1, 11.6, 14.2, 12.1, 13.9, 11.4, 15.1, 13, 11.3, 11.4,
10.4, 14.4, 11, 14, 13.4), success = c(0L, 0L, 0L, 1L, 0L, 1L,
0L, 0L, 1L, 0L, 1L, 1L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L,
1L, 1L, 1L, 0L, 0L, 0L, 1L, 0L, 1L, 0L, 0L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L)), .Names = c("numeracy",
"anxiety", "success"), row.names = c(NA, -50L), class = "data.frame")
attach(A)
names(A)
[1] "numeracy" "anxiety" "success"
head(A)
numeracy anxiety success
1 6.6 13.8 0
2 7.1 14.6 0
3 7.3 17.4 0
4 7.5 14.9 1
5 7.9 13.4 0
6 7.9 13.5 1
The variable ‘success’ is a binary variable that takes the value 1 for individuals who succeeded in gaining admission, and the value 0 for those who did not. Let’s look at the mean values of numeracy and anxiety.
mean(numeracy)
[1] 10.722
mean(anxiety)
[1] 13.954
We begin by fitting a model that includes interactions through the asterisk formula operator. The most commonly used link for binary outcome variables is the logit link, though other links can be used.
model1 <- glm(success ~ numeracy * anxiety, binomial)
glm() is the function that tells R to run a generalized linear model.
Inside the parentheses we give R important information about the model. To the left of the ~ is the dependent variable: success. It must be coded 0 & 1 for glm to read it as binary.
After the ~, we list the two predictor variables. The * indicates that not only do we want each main effect, but we also want an interaction term between numeracy and anxiety.
And finally, after the comma, we specify that the distribution is binomial. The default link function in glm for a binomial outcome variable is the logit. More on that below.
We can access the model output using summary().
summary(model1)
Call:
glm(formula = success ~ numeracy * anxiety, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.85712 -0.33055 0.02531 0.34931 2.01048
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.87883 46.45256 0.019 0.985
numeracy 1.94556 4.78250 0.407 0.684
anxiety -0.44580 3.25151 -0.137 0.891
numeracy:anxiety -0.09581 0.33322 -0.288 0.774
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 28.201 on 46 degrees of freedom
AIC: 36.201
Number of Fisher Scoring iterations: 7
The estimates (coefficients of the predictors – numeracy and anxiety) are now in logits. The coefficient of numeracy is: 1.94556, so that a one unit change in numeracy produces approximately a 1.95 unit change in the log odds (i.e. a 1.95 unit change in the logit).
From the signs of the two predictors, we see that numeracy influences admission positively, but anxiety influences admission negatively.
We can’t tell much more than that as most of us can’t think in terms of logits. Instead we can convert these logits to odds ratios.
We do this by exponentiating each coefficient. (This means raise the value e –approximately 2.72–to the power of the coefficient. e^b).
So, the odds ratio for numeracy is:
OR = exp(1.94556) = 6.997549
However, in this version of the model the estimates are non-significant, and we have a non-significant interaction. Model1 produces the following relationship between the logit (log odds) and the two predictors:
logit(p) = 0.88 + 1.95* numeracy - 0.45 * anxiety - .10* interaction term
The output produced by glm() includes several additional quantities that require discussion.
We see a z value for each estimate. The z value is the Wald statistic that tests the hypothesis that the estimate is zero. The null hypothesis is that the estimate has a normal distribution with mean zero and standard deviation of 1. The quoted p-value, P(>|z|), gives the tail area in a two-tailed test.
For our example, we have a Null Deviance of about 68.03 on 49 degrees of freedom. This value indicates poor fit (a significant difference between fitted values and observed values). Including the independent variables (numeracy and anxiety) decreased the deviance by nearly 40 points on 3 degrees of freedom. The Residual Deviance is 28.2 on 46 degrees of freedom (i.e. a loss of three degrees of freedom).
About the Author: David Lillis has taught R to many researchers and statisticians. His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. David holds a doctorate in applied statistics.
See our full R Tutorial Series and other blog posts regarding R programming.

 Others are about the form of the model. They include linearity and (more…)
Others are about the form of the model. They include linearity and (more…)
 The model has produced a curve that indicates the probability that success = 1 to the numeracy score. Clearly, the higher the score, the more likely it is that the student will be accepted.
The model has produced a curve that indicates the probability that success = 1 to the numeracy score. Clearly, the higher the score, the more likely it is that the student will be accepted. Clearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety.
Clearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety.