In a previous post we explored bounded variables and the difference between truncated and censored. Can we ignore the fact that a variable is bounded and just run our analysis as if the data wasn’t bounded? (more…)
OptinMon 03 - Poisson and Negative Binomial Regression Models
Issues with Truncated Data
May 12th, 2016 by Jeff Meyer
Zero One Inflated Beta Models for Proportion Data
March 16th, 2016 by Karen Grace-Martin
Proportion and percentage data are tricky to analyze.
Much like count data, they look like they should work in a linear model.
They’re numeric. They’re often continuous.
And sometimes they do work. Some proportion data do look normally distributed so estimates and p-values are reasonable.
But more often they don’t. So estimates and p-values are a mess. Luckily, there are other options. (more…)
Generalized Linear Models in R, Part 7: Checking for Overdispersion in Count Regression
August 27th, 2015 by David Lillis
In my last blog post we fitted a generalized linear model to count data using a Poisson error structure.
We found, however, that there was over-dispersion in the data – the variance was larger than the mean in our dependent variable.
Generalized Linear Models in R, Part 6: Poisson Regression for Count Variables
August 26th, 2015 by David Lillis
In my last couple of articles (Part 4, Part 5), I demonstrated a logistic regression model with binomial errors on binary data in R’s glm() function.
But one of wonderful things about glm() is that it is so flexible. It can run so much more than logistic regression models.
The flexibility, of course, also means that you have to tell it exactly which model you want to run, and how.
In fact, we can use generalized linear models to model count data as well.
In such data the errors may well be distributed non-normally and the variance usually increases with the mean values.
As with binary data, we use the glm() command, but this time we specify a Poisson error distribution and the logarithm as the link function.
The natural log is the default link function for the Poisson error distribution. It works well for count data as it forces all of the predicted values to be positive.
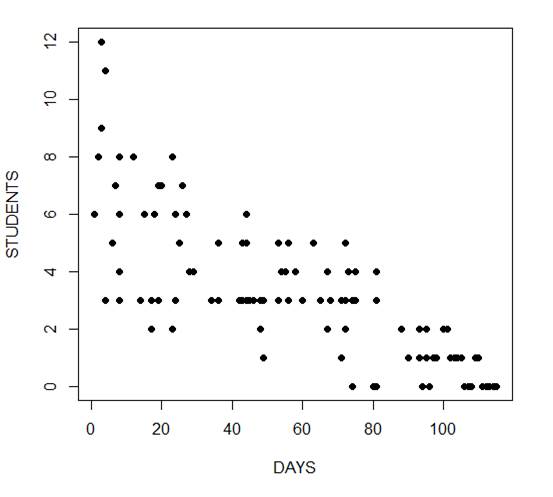
In the following example we fit a generalized linear model to count data using a Poisson error structure. The data set consists of counts of high school students diagnosed with an infectious disease within a period of days from an initial outbreak.
cases <-
structure(list(Days = c(1L, 2L, 3L, 3L, 4L, 4L, 4L, 6L, 7L, 8L,
8L, 8L, 8L, 12L, 14L, 15L, 17L, 17L, 17L, 18L, 19L, 19L, 20L,
23L, 23L, 23L, 24L, 24L, 25L, 26L, 27L, 28L, 29L, 34L, 36L, 36L,
42L, 42L, 43L, 43L, 44L, 44L, 44L, 44L, 45L, 46L, 48L, 48L, 49L,
49L, 53L, 53L, 53L, 54L, 55L, 56L, 56L, 58L, 60L, 63L, 65L, 67L,
67L, 68L, 71L, 71L, 72L, 72L, 72L, 73L, 74L, 74L, 74L, 75L, 75L,
80L, 81L, 81L, 81L, 81L, 88L, 88L, 90L, 93L, 93L, 94L, 95L, 95L,
95L, 96L, 96L, 97L, 98L, 100L, 101L, 102L, 103L, 104L, 105L,
106L, 107L, 108L, 109L, 110L, 111L, 112L, 113L, 114L, 115L),
Students = c(6L, 8L, 12L, 9L, 3L, 3L, 11L, 5L, 7L, 3L, 8L,
4L, 6L, 8L, 3L, 6L, 3L, 2L, 2L, 6L, 3L, 7L, 7L, 2L, 2L, 8L,
3L, 6L, 5L, 7L, 6L, 4L, 4L, 3L, 3L, 5L, 3L, 3L, 3L, 5L, 3L,
5L, 6L, 3L, 3L, 3L, 3L, 2L, 3L, 1L, 3L, 3L, 5L, 4L, 4L, 3L,
5L, 4L, 3L, 5L, 3L, 4L, 2L, 3L, 3L, 1L, 3L, 2L, 5L, 4L, 3L,
0L, 3L, 3L, 4L, 0L, 3L, 3L, 4L, 0L, 2L, 2L, 1L, 1L, 2L, 0L,
2L, 1L, 1L, 0L, 0L, 1L, 1L, 2L, 2L, 1L, 1L, 1L, 1L, 0L, 0L,
0L, 1L, 1L, 0L, 0L, 0L, 0L, 0L)), .Names = c("Days", "Students"
), class = "data.frame", row.names = c(NA, -109L))
attach(cases)
head(cases)
Days Students
1 1 6
2 2 8
3 3 12
4 3 9
5 4 3
6 4 3
The mean and variance are different (actually, the variance is greater). Now we plot the data.
plot(Days, Students, xlab = "DAYS", ylab = "STUDENTS", pch = 16)
Now we fit the glm, specifying the Poisson distribution by including it as the second argument.
model1 <- glm(Students ~ Days, poisson) summary(model1) Call: glm(formula = Students ~ Days, family = poisson) Deviance Residuals: Min 1Q Median 3Q Max -2.00482 -0.85719 -0.09331 0.63969 1.73696 Coefficients: Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.990235 0.083935 23.71 <2e-16 ***
Days -0.017463 0.001727 -10.11 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 215.36 on 108 degrees of freedom
Residual deviance: 101.17 on 107 degrees of freedom
AIC: 393.11
Number of Fisher Scoring iterations: 5
The negative coefficient for Days indicates that as days increase, the mean number of students with the disease is smaller.
This coefficient is highly significant (p < 2e-16).
We also see that the residual deviance is greater than the degrees of freedom, so that we have over-dispersion. This means that there is extra variance not accounted for by the model or by the error structure.
This is a very important model assumption, so in my next article we will re-fit the model using quasi poisson errors.
****
See our full R Tutorial Series and other blog posts regarding R programming.
About the Author: David Lillis has taught R to many researchers and statisticians. His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. David holds a doctorate in applied statistics.
When Can Count Data be Considered Continuous?
January 13th, 2012 by Karen Grace-Martin
Last month I did a webinar on Poisson and negative binomial models for count data. With a few hundred participants, we ran out of time to get through all the questions, so I’m answering some of them here on the blog.
This set of questions are all related to when it’s appropriate to treat count data as continuous and run the more familiar and simpler linear model.
Q: Do you have any guidelines or rules of thumb as far as how many discrete values an outcome variable can take on before it makes more sense to just treat it as continuous?
The issue usually isn’t a matter of how many values there are.
A Few Resources on Zero-Inflated Poisson Models
February 15th, 2010 by Karen Grace-Martin
1. For a general overview of modeling count variables, you can get free access to the video recording of one of my The Craft of Statistical Analysis Webinars:
Poisson and Negative Binomial for Count Outcomes
2. One of my favorite books on Categorical Data Analysis is:
Long, J. Scott. (1997). Regression models for Categorical and Limited Dependent Variables. Sage Publications.
It’s moderately technical, but written with social science researchers in mind. It’s so well written, it’s worth it. It has a section specifically about Zero Inflated Poisson and Zero Inflated Negative Binomial regression models.
3. Slightly less technical, but most useful only if you use Stata is >Regression Models for Categorical Dependent Variables Using Stata, by J. Scott Long and Jeremy Freese.
4. UCLA’s ATS Statistical Software Consulting Group has some nice examples of Zero-Inflated Poisson and other models in various software packages.