In a statistical model–any statistical model–there is generally one way that a predictor X and a response Y can relate:
This relationship can take on different forms, of course, like a line or a curve, but there’s really only one relationship here to measure.
Usually the point is to model the predictive ability, the effect, of X on Y.
In other words, there is a clear response variable*, although not necessarily a causal relationship. We could have switched the direction of the arrow to indicate that Y predicts X or used a two-headed arrow to show a correlation, with no direction, but that’s a whole other story.
For our purposes, Y is the response variable and X the predictor.
But a third variable–another predictor–can relate to X and Y in a number of different ways. How this predictor relates to X and Y changes how we interpret the relationship between X and Y. (more…)
There are two oft-cited assumptions for Analysis of Covariance (ANCOVA), which is used to assess the effect of a categorical independent variable on a numerical dependent variable while controlling for a numerical covariate:
1. The independent variable and the covariate are independent of each other.
2. There is no interaction between independent variable and the covariate.
In a previous post, I showed a detailed example for an observational study where the first assumption is irrelevant, but I have gotten a number of questions about the second.
So what does it mean, and what should you do, if you find an interaction between the categorical IV and the continuous covariate? (more…)
In Part 3 we used the lm() command to perform least squares regressions. In Part 4 we will look at more advanced aspects of regression models and see what R has to offer.
One way of checking for non-linearity in your data is to fit a polynomial model and check whether the polynomial model fits the data better than a linear model. However, you may also wish to fit a quadratic or higher model because you have reason to believe that the relationship between the variables is inherently polynomial in nature. Let’s see how to fit a quadratic model in R.
We will use a data set of counts of a variable that is decreasing over time. Cut and paste the following data into your R workspace.
A <- structure(list(Time = c(0, 1, 2, 4, 6, 8, 9, 10, 11, 12, 13,
14, 15, 16, 18, 19, 20, 21, 22, 24, 25, 26, 27, 28, 29, 30),
Counts = c(126.6, 101.8, 71.6, 101.6, 68.1, 62.9, 45.5, 41.9,
46.3, 34.1, 38.2, 41.7, 24.7, 41.5, 36.6, 19.6,
22.8, 29.6, 23.5, 15.3, 13.4, 26.8, 9.8, 18.8, 25.9, 19.3)), .Names = c("Time", "Counts"),
row.names = c(1L, 2L, 3L, 5L, 7L, 9L, 10L, 11L, 12L, 13L, 14L, 15L, 16L, 17L, 19L, 20L, 21L, 22L, 23L, 25L, 26L, 27L, 28L, 29L, 30L, 31L),
class = "data.frame")
Let’s attach the entire dataset so that we can refer to all variables directly by name.
attach(A)
names(A)
First, let’s set up a linear model, though really we should plot first and only then perform the regression.
linear.model <-lm(Counts ~ Time)
We now obtain detailed information on our regression through the summary() command.
summary(linear.model)
Call:
lm(formula = Counts ~ Time)
Residuals:
Min 1Q Median 3Q Max
-20.084 -9.875 -1.882 8.494 39.445
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 87.1550 6.0186 14.481 2.33e-13 ***
Time -2.8247 0.3318 -8.513 1.03e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.16 on 24 degrees of freedom
Multiple R-squared: 0.7512, Adjusted R-squared: 0.7408
F-statistic: 72.47 on 1 and 24 DF, p-value: 1.033e-08
The model explains over 74% of the variance and has highly significant coefficients for the intercept and the independent variable and also a highly significant overall model p-value. However, let’s plot the counts over time and superpose our linear model.
plot(Time, Counts, pch=16, ylab = "Counts ", cex.lab = 1.3, col = "red" )
abline(lm(Counts ~ Time), col = "blue")
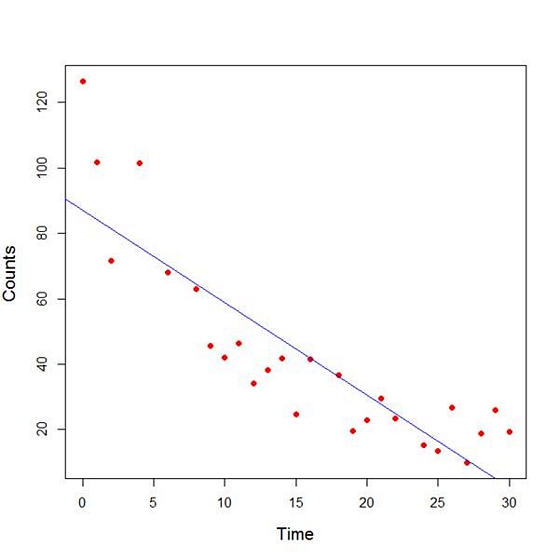
Here the syntax cex.lab = 1.3 produced axis labels of a nice size.
The model looks good, but we can see that the plot has curvature that is not explained well by a linear model. Now we fit a model that is quadratic in time. We create a variable called Time2 which is the square of the variable Time.
Time2 <- Time^2
quadratic.model <-lm(Counts ~ Time + Time2)
Note the syntax involved in fitting a linear model with two or more predictors. We include each predictor and put a plus sign between them.
summary(quadratic.model)
Call:
lm(formula = Counts ~ Time + Time2)
Residuals:
Min 1Q Median 3Q Max
-24.2649 -4.9206 -0.9519 5.5860 18.7728
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 110.10749 5.48026 20.092 4.38e-16 ***
Time -7.42253 0.80583 -9.211 3.52e-09 ***
Time2 0.15061 0.02545 5.917 4.95e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.754 on 23 degrees of freedom
Multiple R-squared: 0.9014, Adjusted R-squared: 0.8928
F-statistic: 105.1 on 2 and 23 DF, p-value: 2.701e-12
Our quadratic model is essentially a linear model in two variables, one of which is the square of the other. We see that however good the linear model was, a quadratic model performs even better, explaining an additional 15% of the variance. Now let’s plot the quadratic model by setting up a grid of time values running from 0 to 30 seconds in increments of 0.1s.
timevalues <- seq(0, 30, 0.1)
predictedcounts <- predict(quadratic.model,list(Time=timevalues, Time2=timevalues^2))
plot(Time, Counts, pch=16, xlab = "Time (s)", ylab = "Counts", cex.lab = 1.3, col = "blue")
Now we include the quadratic model to the plot using the lines() command.
lines(timevalues, predictedcounts, col = "darkgreen", lwd = 3)
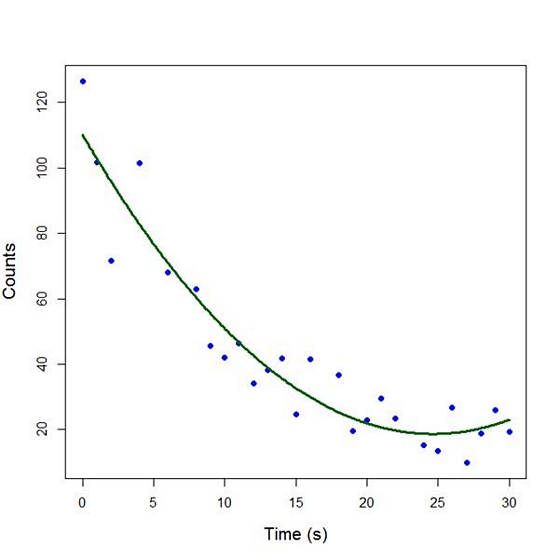
The quadratic model appears to fit the data better than the linear model. We will look again at fitting curved models in our next blog post.
About the Author: David Lillis has taught R to many researchers and statisticians. His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. David holds a doctorate in applied statistics.
See our full R Tutorial Series and other blog posts regarding R programming.
You may have noticed conflicting advice about whether to leave insignificant effects in a model or take them out in order to simplify the model.
One effect of leaving in insignificant predictors is on p-values–they use up precious df in small samples. But if your sample isn’t small, the effect is negligible.
The bigger effect is on interpretation, and really the above cases are about whether it aids interpretation to leave them in. Models do get so cluttered it’s hard to figure out what’s going on, and it makes sense to eliminate effects that aren’t serving a purpose, but even insignificant effects can have a purpose. (more…)
“Everything should be made as simple as possible, but no simpler” – Albert Einstein*
For some reason, I’ve heard this quotation 3 times in the past 3 days. Maybe I hear it everyday, but only noticed because I’ve been working with a few clients on model selection, and deciding how much to simplify a model.
And when the quotation fits, use it. (That’s the saying, right?)
*For the record, a quick web search indicated this may be a paraphrase, but it still applies.
The quotation is the general goal of model selection. You really do want the model to be as simple as possible, but still able to answer the research question of interest.
This applies to many areas of model selection. Here are a few examples: (more…)
