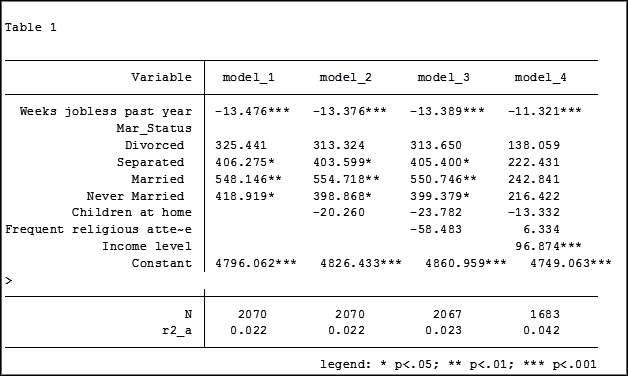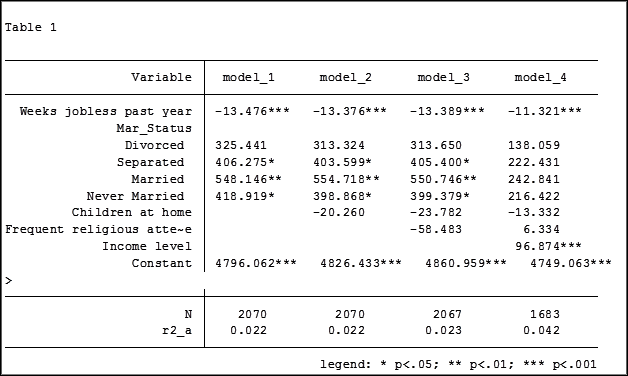OptinMon 30 - Four Critical Steps in Building Linear Regression Models

There are not a lot of statistical methods designed just for ordinal variables.

But that doesn’t mean that you’re stuck with few options.  There are more than you’d think. (more…)

3 comments

You put a lot of work into preparing and cleaning your data. Running the model is the moment of excitement.

You look at your tables and interpret the results. But first you remember that one or more variables had a few outliers. Did these outliers impact your results? (more…)

No comments yet

In a previous post , Using the Same Sample for Different Models in Stata, we examined how to use the same sample when comparing regression models. Using different samples in our models could lead to erroneous conclusions when interpreting results.

But excluding observations can also result in inaccurate results.

The coefficient for the variable “frequent religious attendance” was negative 58 in model 3 (more…)

No comments yet

In my last article, Hierarchical Regression in Stata: An Easy Method to Compare Model Results, I presented the following table which examined the impact several predictors have on one’ mental health.

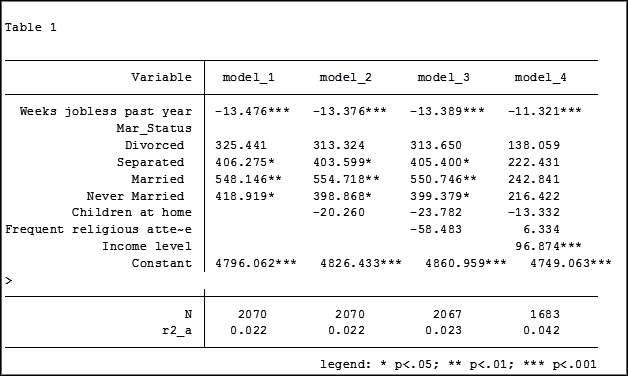
At the bottom of the table is the number of observations (N) contained within each sample.

The sample sizes are quite large. Does it really matter that they are different? The answer is absolutely yes.

Fortunately in Stata it is not a difficult process to use the same sample for all four models shown above.

Some background info:

As I have mentioned previously, Stata stores results in temp files. You don’t have to do anything to cause Stata to store these results, but if you’d like to use them, you need to know what they’re called.

To see what is stored after an estimation command, use the following code:
ereturn list

After a summary command:
return list

One of the stored results after an estimation command is the function e(sample). e(sample) returns a one column matrix.  If an observation is used in the estimation command it will have a value of 1 in this matrix. If it is not used it will have a value of 0.

Remember that the “stored” results are in temp files.  They will disappear the next time you run another estimation command.

The Steps

So how do I use the same sample for all my models? Follow these steps.

Using the regression example on mental health I determine which model has the fewest observations.  In this case it was model four.

I rerun the model:
regress MCS  weeks_unemployed   i.marital_status   kids_in_house  religious_attend    income

Next I use the generate command to create a new variable whose value is 1 if the observation was in the model and 0 if the observation was not. I will name the new variable “in_model_4”.
gen in_model_4 = e(sample)

Now I will re-run my four regressions and include only the observations that were used in model 4. I will store the models using different names so that I can compare them to the original models.

My commands to run the models are:

regress MCS  weeks_unemployed   i.marital_status  if  in_model_4==1
estimates store model_1a

regress MCS  weeks_unemployed   i.marital_status   kids_in_house  if  in_model_4==1
estimates store model_2a

regress MCS  weeks_unemployed   i.marital_status   kids_in_house   religious_attend if  in_model_4==1
estimates store model_3a

regress MCS  weeks_unemployed   i.marital_status   kids_in_house  religious_attend    income if  in_model_4==1
estimates store model_4a

Note: I could use the code  if  in_model_4 instead of if  in_model_4==1. Stata interprets dummy variables as 0 = false, 1 = true.

Here are the results comparing the original models (eg. Model_1) versus the models using the same sample (eg. Model_1a):

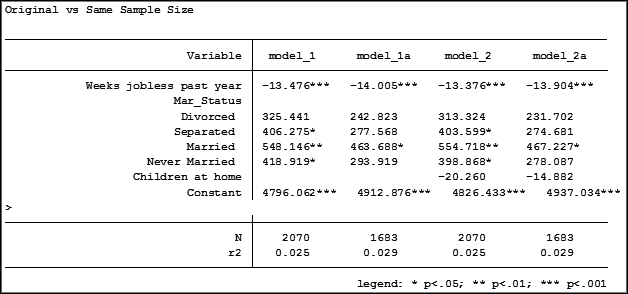
Comparing the original models 3 and 4 one would have assumed that the predictor variable “Income level” significantly impacted the coefficient of “Frequent religious attendance”. Its coefficient changed from -58.48 in model 3 to 6.33 in model 4.

That would have been the wrong assumption. That change is coefficient was not so much about any effect of the variable itself, but about the way it causes the sample to change via listwise deletion.  Using the same sample, the change in the coefficient between the two models is very small, moving from 4 to 6.

No comments yet

An “estimation command” in Stata is a generic term used for a command that runs a statistical model. Examples are regress, ANOVA, Poisson, logit, and mixed.

Stata has more than 100 estimation commands.

Creating the “best” model requires trying alternative models.  There are a number of different model building approaches, but regardless of the strategy you take, you’re going to need to compare them.

Running all these models can generate a fair amount of output to compare and contrast. How can you view and keep track of all of the results?

You could scroll through the results window on your screen. But this method makes it difficult to compare differences.

You could copy and paste the results into a Word document or spreadsheet. Or better yet use the “esttab” command to output your results.  But both of these require a number of time consuming steps.

But Stata makes it easy: my suggestion is to use the post-estimation command “estimates”.

What is a post-estimation command?  A post-estimation command analyzes the stored results of an estimation command (regress, ANOVA, etc).

As long as you give each model a different name you can store countless results (Stata stores the results as temp files).  You can then use post-estimation commands to dig deeper into the results of that specific estimation.

Here is an example.  I will run four regression models to examine the impact several factors have on one’s mental health (Mental Composite Score). I will then store the results of each one.

regress MCS  weeks_unemployed   i.marital_status
estimates store model_1

regress MCS  weeks_unemployed   i.marital_status   kids_in_house
estimates store model_2

regress MCS  weeks_unemployed   i.marital_status   kids_in_house   religious_attend
estimates store model_3

regress MCS  weeks_unemployed   i.marital_status   kids_in_house  religious_attend    income
estimates store model_4

To view the results of the four models in one table my code can be as simple as:

estimates table model_1 model_2 model_3 model_4

But I want to format it so I use the following:

estimates table model_1 model_2 model_3 model_4, varlabel varwidth(25)  b(%6.3f) /// star(0.05 0.01 0.001) stats(N r2_a)

Here are my results:

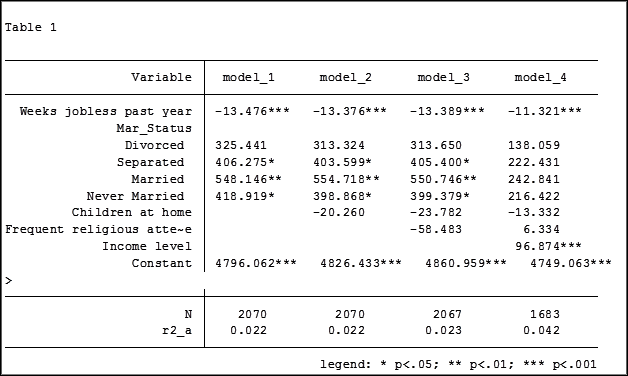
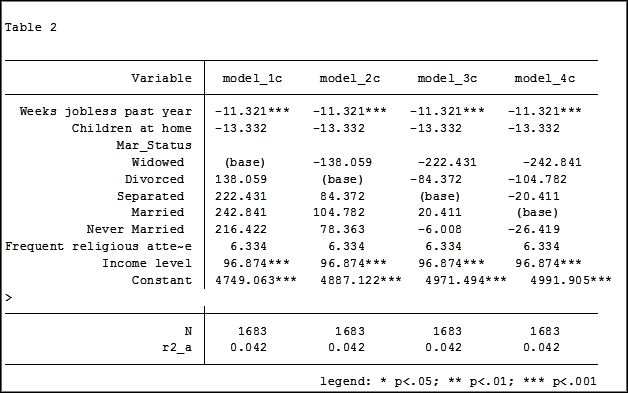
My base category for marital status was “widowed”. Is “widowed” the base category I want to use in my final analysis? I can easily re-run model 4, using a different reference group base category each time.

Putting the results into one table will make it easier for me to determine which category to use as the base.

Note in table 1 the size of the samples have changed from model 2 (2,070) to model 3 (2,067) to model 4 (1,682). In the next article we will explore how to use post-estimation data to use the same sample for each model.
Jeff Meyer is a statistical consultant with The Analysis Factor, a stats mentor for Statistically Speaking membership, and a workshop instructor. Read more about Jeff here.

16 comments

Last time we created two variables and used the lm() command to perform a least squares regression on them, and diagnosing our regression using the plot() command.

Just as we did last time, we perform the regression using lm(). This time we store it as an object M. (more…)

No comments yet