The normal distribution is so ubiquitous in statistics that those of us who use a lot of statistics tend to forget it’s not always so common in actual data.
And since the normal distribution is continuous, many people describe all numerical variables as continuous. I get it: I’m guilty of using those terms interchangeably, too, but they’re not exactly the same.
Numerical variables can be either continuous or discrete.
The difference? Continuous variables can take any number within a range. Discrete variables can only take on specific values. For numeric discrete data, these are often, but don’t have to be, whole numbers*.
Count variables, as the name implies, are frequencies of some event or state. Number of arrests, fish (more…)
Outliers are one of those realities of data analysis that no one can avoid.
Those pesky extreme values cause biased parameter estimates, non-normality in otherwise beautifully normal variables, and inflated variances.
Everyone agrees that outliers cause trouble with parametric analyses. But not everyone agrees that they’re always a problem, or what to do about them even if they are.
Sometimes a nonparametric or robust alternative is available — and sometimes not.
There are a number of approaches in statistical analysis for dealing with outliers and the problems they create. It’s common for committee members or Reviewer #2 to have very strong opinions that there is one and only one good approach.
Two approaches that I’ve commonly seen are: 1) delete outliers from the sample, or 2) winsorize them (i.e., replace the outlier value with one that is less extreme).
The problem with both of these “solutions” is that they also cause problems — biased parameter estimates and underweighted or eliminated valid values. (more…)
A common situation with count outcome variables is there are a lot of zero values. The Poisson distribution used for modeling count variables takes into account that zeros are often the most
common value, but sometimes there are even more zeros than the Poisson distribution can account for.
This can happen in continuous variables as well–most of the distribution follows a beautiful normal distribution, except for the big stack of zeros.
This webinar will explore two ways of modeling zero-inflated data: the Zero Inflated model and the Hurdle model. Both assume there are two different processes: one that affects the probability of a zero and one that affects the actual values, and both allow different sets of predictors for each process.
We’ll explore these models as well as some related models, like Zero-One Inflated Beta models for proportion data.
Note: This training is an exclusive benefit to members of the Statistically Speaking Membership Program and part of the Stat’s Amore Trainings Series. Each Stat’s Amore Training is approximately 90 minutes long.
(more…)
Proportion and percentage data are tricky to analyze.
Much like count data, they look like they should work in a linear model.
They’re numeric. They’re often continuous.
And sometimes they do work. Some proportion data do look normally distributed so estimates and p-values are reasonable.
But more often they don’t. So estimates and p-values are a mess. Luckily, there are other options. (more…)
Like the chicken and the egg, there’s a question about which comes first: run a model or test assumptions? Unlike the chicken’s, the model’s question has an easy answer.
There are two types of assumptions in a statistical model. Some are distributional assumptions about the errors. Examples include independence, normality, and constant variance in a linear model.
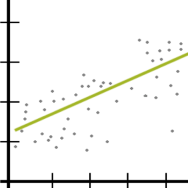Others are about the form of the model. They include linearity and (more…)
One common reason for running Principal Component Analysis (PCA) or Factor Analysis (FA) is variable reduction.
In other words, you may start with a 10-item scale meant to measure something like Anxiety, which is difficult to accurately measure with a single question.
You could use all 10 items as individual variables in an analysis–perhaps as predictors in a regression model.
But you’d end up with a mess.
Not only would you have trouble interpreting all those coefficients, but you’re likely to have multicollinearity problems.
And most importantly, you’re not interested in the effect of each of those individual 10 items on your (more…)
