Repeated measures is one of those terms in statistics that sounds like it could apply to many design situations. In fact, it describes only one.
A repeated measures design is one where each subject is measured repeatedly over time, space, or condition on the dependent variable.
These repeated measurements on the same subject are not independent of each other. They’re clustered. They are more correlated to each other than they are to responses from other subjects. Even if both subjects are in the same condition. (more…)
There are important ‘rules’ of statistical analysis. Like
- Always run descriptive statistics and graphs before running tests
- Use the simplest test that answers the research question and meets assumptions
- Always check assumptions.
But there are others you may have learned in statistics classes that don’t serve you or your analysis well once you’re working with real data.
When you are taking statistics classes, there is a lot going on. You’re learning concepts, vocabulary, and some really crazy notation. And probably a software package on top of that.
In other words, you’re learning a lot of hard stuff all at once.
Good statistics professors and textbook authors know that learning comes in stages. Trying to teach the nuances of good applied statistical analysis to students who are struggling to understand basic concepts results in no learning at all.
And yet students need to practice what they’re learning so it sticks. So they teach you simple rules of application. Those simple rules work just fine for students in a stats class working on sparkling clean textbook data.
But they are over-simplified for you, the data analyst, working with real, messy data.
Here are three rules of data analysis practice that you may have learned in classes that you need to unlearn. They are not always wrong. They simply don’t allow for the nuance involved in real statistical analysis.
The Rules of Statistical Analysis to Unlearn:
1. To check statistical assumptions, run a test. Decide whether the assumption is met by the significance of that test.
Every statistical test and model has assumptions. They’re very important. And they’re not always easy to verify.
For many assumptions, there are tests whose sole job is to test whether the assumption of another test is being met. Examples include the Levene’s test for constant variance and Kolmogorov-Smirnov test, often used for normality. These tests are tools to help you decide if your model assumptions are being met.
But they’re not definitive.
When you’re checking assumptions, there are a lot of contextual issues you need to consider: the sample size, the robustness of the test you’re running, the consequences of not meeting assumptions, and more.
What to do instead:
Use these test results as one of many pieces of information that you’ll use together to decide whether an assumption is violated.
2. Delete outliers that are 3 or more standard deviations from the mean.
This is an egregious one. Really. It’s bad.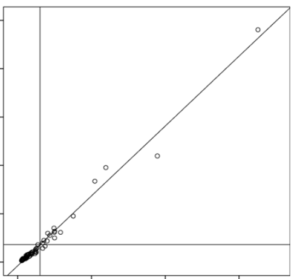
Yes, it makes the data look pretty. Yes, there are some situations in which it’s appropriate to delete outliers (like when you have evidence that it’s an error). And yes, outliers can wreak havoc on your parameter estimates.
But don’t make it a habit. Don’t follow a rule blindly.
Deleting outliers because they’re outliers (or using techniques like Winsorizing) is a great way to introduce bias into your results or to miss the most interesting part of your data set.
What to do instead:
When you find an outlier, investigate it. Try to figure out if it’s an error. See if you can figure out where it came from.
3. Check Normality of Dependent Variables before running a linear model
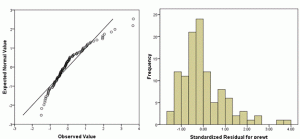 In a t-test, yes, there is an assumption that Y, the dependent variable, is normally distributed within each group. In other words, given the group as defined by X, Y follows a normal distribution.
In a t-test, yes, there is an assumption that Y, the dependent variable, is normally distributed within each group. In other words, given the group as defined by X, Y follows a normal distribution.
ANOVA has a similar assumption: given the group as defined by X, Y follows a normal distribution.
In linear regression (and ANCOVA), where we have continuous variables, this same assumption holds. But it’s a little more nuanced since X is not necessarily categorical. At any specific value of X, Y has a normal distribution. (And yes, this is equivalent to saying the errors have a normal distribution).
But here’s the thing: the distribution of Y as a whole doesn’t have to be normal.
In fact, if X has a big effect, the distribution of Y, across all values of X, will often be skewed or bimodal or just a big old mess. This happens even if the distribution of Y, at each value of X, is perfectly normal.
What to do instead:
Because normality depends on which Xs are in a model, check assumptions after you’ve chosen predictors.
Conclusion:
The best rule in statistical analysis: always stop and think about your particular data analysis situation.
If you don’t understand or don’t have the experience to evaluate your situation, discuss it with someone who does. Investigate it. This is how you’ll learn.
Of all the stressors you’ve got right now, accessing your statistical software from home shouldn’t be one of them. (You know, the one on your office computer).
We’ve gotten some updates from some statistical software companies on how they’re making it easier to access the software you have a license to or to extend a free trial while you’re working from home.
(more…)
One activity in data analysis that can seem impossible is the quest to find the right analysis. I applaud the conscientiousness and integrity that  underlies this quest.
underlies this quest.
The problem: in many data situations there isn’t one right analysis.
(more…)
Odds is confusing in a different way than some of the other terms in this series.
First, it’s a bit of an abstract concept, which I’ll explain below.
But beyond that, it’s confusing because it is used in everyday English as a synonym for probability, but it’s actually a distinct technical term.
I found this incorrect definition recently in a (non-statistics) book: (more…)

Multicollinearity is one of those terms in statistics that is often defined in one of two ways:
1. Very mathematical terms that make no sense — I mean, what is a linear combination anyway?
2. Completely oversimplified in order to avoid the mathematical terms — it’s a high correlation, right?
So what is it really? In English?
(more…)



