Sometimes what is most tricky about understanding your regression output is knowing exactly what your software is presenting to you.
Here’s a great example of what looks like two completely different model results from SPSS and Stata that in reality, agree.
The Model
I ran a linear model regressing “physical composite score” on education and “mental composite score”.
The outcome variable, physical composite score, is a measurement of one’s physical well-being. The predictor “education” is categorical with four categories. The other predictor, mental composite score, is continuous and measures one’s mental well-being.
I am interested in determining whether the association between physical composite score and mental composite score is different among the four levels of education. To determine this I included an interaction between mental composite score and education.
The SPSS Regression Output
Here is the result of the regression using SPSS:
(more…)
Linear regression with a continuous predictor is set up to measure the constant relationship between that predictor and a continuous outcome.
This relationship is measured in the expected change in the outcome for each one-unit change in the predictor.
One big assumption in this kind of model, though, is that this rate of change is the same for every value of the predictor. It’s an assumption we need to question, though, because it’s not a good approach for a lot of relationships.
Segmented regression allows you to generate different slopes and/or intercepts for different segments of values of the continuous predictor. This can provide you with a wealth of information that a non-segmented regression cannot.
In this webinar, we will cover (more…)
It’s that time of year: flu season.
Let’s imagine you have been asked to determine the factors that will help a hospital determine the length of stay in the intensive care unit (ICU) once a patient is admitted.
The hospital tells you that once the patient is admitted to the ICU, he or she has a day count of one. As soon as they spend 24 hours plus 1 minute, they have stayed an additional day.
Clearly this is count data. There are no fractions, only whole numbers.
To help us explore this analysis, let’s look at real data from the State of Illinois. We know the patients’ ages, gender, race and type of hospital (state vs. private).
A partial frequency distribution looks like this: (more…)
In a previous article, we discussed how incidence rate ratios calculated in a Poisson regression can be determined from a two-way table of categorical variables.
Statistical software can also calculate the expected (aka predicted) count for each group. Below is the actual and expected count of the number of boys and girls participating and not participating in organized sports.
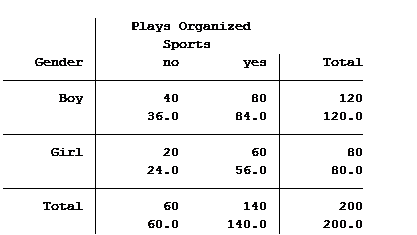
The value in the top of each cell is the actual count (40 boys do not play organized sports) and the bottom value is the expected/predicted count (36 boys are predicted to not play organized sports).
The Poisson model that we ran in the previous article generated the following table: (more…)
The coefficients of count model regression tables are shown in either logged form or as incidence rate ratios. Trying to explain the coefficients in logged form can be a difficult process.
Incidence rate ratios are much easier to explain. You probably didn’t realize you’ve seen incidence rate ratios before, expressed differently.
Let’s look at an example.
A school district was interested in how many children in their sixth grade classes played on organized sports teams. So they did a count and also noted the gender of the child. The results were put into a table: (more…)
If you have count data you use a Poisson model for the analysis, right?
The key criterion for using a Poisson model is after accounting for the effect of predictors, the mean must equal the variance. If the mean doesn’t equal the variance then all we have to do is transform the data or tweak the model, correct?
Let’s see how we can do this with some real data. A survey was done in Australia during the peak of the flu season. The outcome variable is the total number of times people asked for medical advice from any source over a two-week period.
We are trying to determine what influences people with flu symptoms to seek medical advice. The mean number of times was 0.516 times and the variance 1.79.
The mean does not equal the variance even after accounting for the model’s predictors.
Here are the results for this model: (more…)