How do you choose between Poisson and negative binomial models for discrete count outcomes?
One key criterion is the relative value of the variance to the mean after accounting for the effect of the predictors. A previous article discussed the concept of a variance that is larger than the model assumes: overdispersion.
(Underdispersion is also possible, but much less common).
There are two ways to check for overdispersion: (more…)
We previously examined why a linear regression and negative binomial regression were not viable models for predicting the expected length of stay in the hospital for people with the flu. A linear regression model was not appropriate because our outcome variable, length of stay, was discrete and not continuous.
A negative binomial model wasn’t the proper choice because the minimum length of stay is not zero. The minimum length of stay is one day. Negative binomial and Poisson models can only be used on data where the observations’ outcome have the possibility of having a zero count.
We need to use a truncated negative binomial model to analyze the expected length of stay of people admitted to the hospital who have the flu. Calculating the expected length of stay is an easy task once we create our model. (more…)
Imagine this scenario:
This year’s flu strain is very vigorous. The number of people checking in at hospitals is rapidly increasing. Hospitals are desperate to know if they have enough beds to handle those who need their help.
You have been asked to analyze a previous year’s hospitalization length of stay by people with the flu who had been admitted to the hospital. The predictors in your data set are age group, gender and race of those admitted. You also have an indicator that signifies whether the hospital was privately or publicly run.
Interpreting regression coefficients can be tricky, especially when the model has interactions or categorical predictors (or worse – both).
But there is a secret weapon that can help you make sense of your regression results: marginal means.
They’re not the same as descriptive stats. They aren’t usually included by default in our output. And they sometimes go by the name LS or Least-Square means.
And they’re your new best friend.
So what are these mysterious, helpful creatures?
What do they tell us, really? And how can we use them?
In a previous post we discussed using marginal means to explain an interaction to a non-statistical audience. The output from a linear regression model can be a bit confusing. This is the model that was shown.
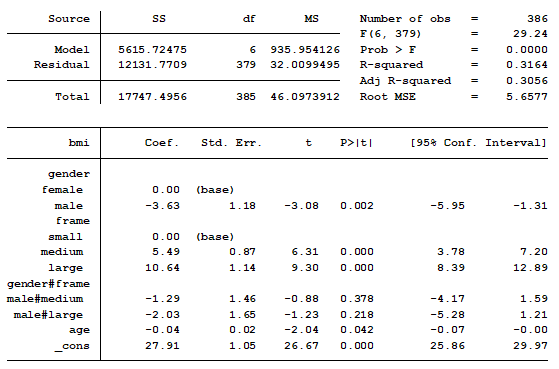
In this model, BMI is the outcome variable and there are three predictors:
When you put a continuous predictor into a linear regression model, you assume it has a constant relationship with the dependent variable along the predictor’s range. But how can you be certain? What is the best way to measure this?
And most important, what should you do if it clearly isn’t the case?
Let’s explore a few options for capturing a non-linear relationship between X and Y within a linear regression (yes, really). (more…)