SPSS has a nice little feature for adding and averaging variables with  missing data that many people don’t know about.
missing data that many people don’t know about.
It allows you to add or average variables that have some missing data, while specifying how many are allowed to be missing.
For example, a very common situation is a researcher needs to average the values of the 5 variables on a scale, each of which is measured on the same Likert scale.
There are a few different ways to do this in SPSS syntax or in the Transform –> Compute menu. The important thing to know is you’ll get different outcomes depending on how you do it.
So let’s look at three methods for averaging variables in SPSS when you have missing data.
Method 1: Adding and dividing to create the mean
One option is to simply compute the mean by following the formula: add up the variables and divide by n, the sample size.
Newvar1=(X1 + X2 + X3 + X4 + X5)/5
In the first method, if any of the variables are missing, Newvar1 will also be missing.
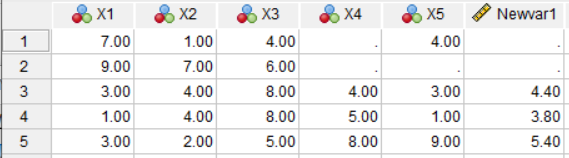
Here’s a simple example. I have five variables, X1 to X5, and five cases in SPSS.
Case 1 is missing one value: X4.
Case 2 is missing two values: X4 and X5.
Cases 3-5 have complete data.
I used the following syntax to create NewVar1:
Compute Newvar1=(X1 + X2 + X3 + X4 + X5)/5.
As you see in the screenshot, both cases 1 and 2 show missing values for NewVar1 because each is missing at least one value. Cases 3 – 5 all have a computed value.
So if you find you only want a value computed if all data are complete, use this method.
Method 2: Averaging with the mean Function
There is an alternative which will give you a lot more data to work with. And that is to use SPSS’s mean function instead of adding and dividing by n yourself.
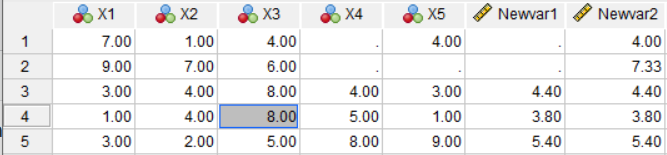
Newvar2=MEAN(X1,X2, X3, X4, X5).
In the second method, if any of the values is missing, SPSS will still calculate the mean.
You can see below that all 5 cases have a value for Newvar2.
While this seems great at first, you want to think about this before you do it.
If only one or two variables have values for a case, the mean may not be a reasonable estimate of the mean of all 5 variables.
Method 3: The mean.n Function
SPSS has an option for dealing with averaging variables with missing data. You may wish to limit how many of the 5 variables need to be observed in order to calculate the mean.
Running it the following way will only calculate the mean if any 4 of the 5 variables are observed. If fewer than 4 of the variables are observed, Newvar4 will be system missing.
Newvar4=MEAN.4(X1,X2, X3, X4, X5).
You can specify any number of variables that need to be observed by choosing any value after that dot. For example:
Newvar3 =MEAN.3(X1,X2, X3, X4, X5).
In the screenshot above, you can see that Newvar3 has a value for all five cases because every case had at least three values.
But not Newvar4. Case 2, with observed data for only three variables, doesn’t get a mean computed. We specified calculating a mean only if there are a minimum of four variables with observed data.
How many observed values do you need?
I’ve added this section based on a number of questions in the comments about how to decide how many variables need to be observed to calculate the mean.
This is one of those situations where there is no clear answer.
For example, if the items are part of a well-constructed and well-tested scale with no sub-scales, the values may quite similar to each other. In that case you may be able to get away with a smaller percentage of observed variables.
But say, for example, you’re taking the average number of times that a participant did a behavior each week for 10 weeks. And there’s a lot of variation from week to week. In that case, you may want to make sure you have almost all the data for each case.
Whatever you choose, be transparent about what you did and why.
Adding
This same distinction holds for adding variables.
Method one, simply add using plus signs. Listwise deletion will drop the case if any values are missing.
Method two, use the SUM function. If at least one variable is present, it will sum whatever is available.
Method three, use the SUM.n function. As long as at least n variables are observed, it will sum whatever is available.
But you really want to pause before you use method 2 or 3 with a sum. It really depends on what the sum is for and why the data are missing.
In some situations, like the data are the number of times an event occurred for that subject, and you’re trying to get a sum of the minimum number of events that occurred for that subject, method 2 could work.
But if you’re adding 10 items on a personality scale and some are missing, you won’t know if the sum is low because there are values missing or if the person scored low values on every item. You may not be measuring what you intend to.
A better approach is to calculate the mean using something like mean.4, then multiply by 5. This will rescale the sum to be comparable to those where all 5 questions were answered.
A note about mean
I’ve added this section based on a number of comments we’ve received over the years about how to then use this for imputing the mean to those missing values.
First, I’ll mention that this is different from mean imputation, which is calculating the mean of one variable across all the subjects. Here we’re talking about calculating each subjects’ mean across a number of similar variables.
It’s important to say that while simple, mean imputation is bad practice. Don’t do it.
Second, imputing this subject-specific mean back into the missing values is both unneeded and also not a good practice. You’re computing this mean to use it instead of the original values.
If not, then having the mean in place of one or more variables will not affect the mean, but it will affect variances and correlations. If you need correlations for something like an exploratory factor analysis, you’re better off using something like the EM algorithm to estimate the correlation matrix and base the factor analysis on that.
First Published 8/29/2008;
Updated 12/17/24 to give more detail.



Leave a Reply